Compilation

Teknik tranlasasi dari satu bahasa pemograman ke bahasa pemograman lain.

Source Language -> Compiler (Compilation) -> Target Language

Regular Expression

1. Variables
2. Symbols:
   • | -> OR, e.g. A|B can result in either be A or B
   • . -> AND, e.g. A.B results in AB
3. Closure
   • *, e.g. a* --> empty, a, aa, aaa, aaa...
   • +, e.g. a+ --> a, aa, aaa, aaa...
   • ?, e.g. a? --> empty, a (no repeats)

Finite Automata

Mesin automata untuk mengecek apakah input dan output sudah sesuai

• Deterministic Finite Automata (DFA)
• Non-deterministic Finite Automata (NFA)
  Finite automata is a collection of states:
  
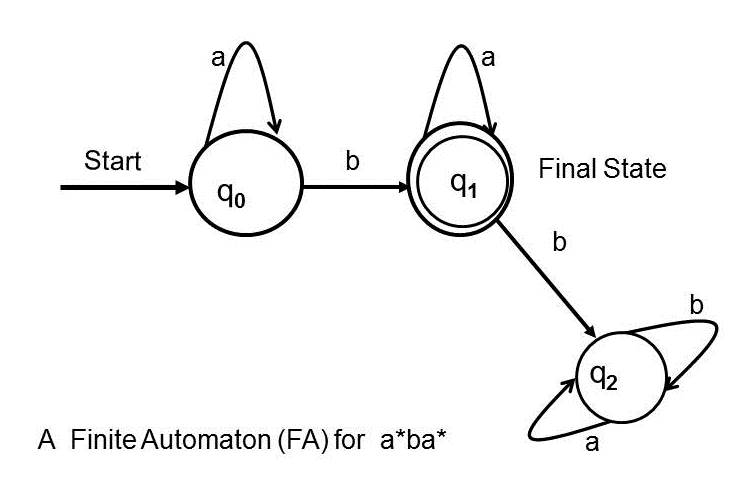
• Arrow represents input, value from regex
• There can be more than one final state
• Start state can either be a normal state or a final state

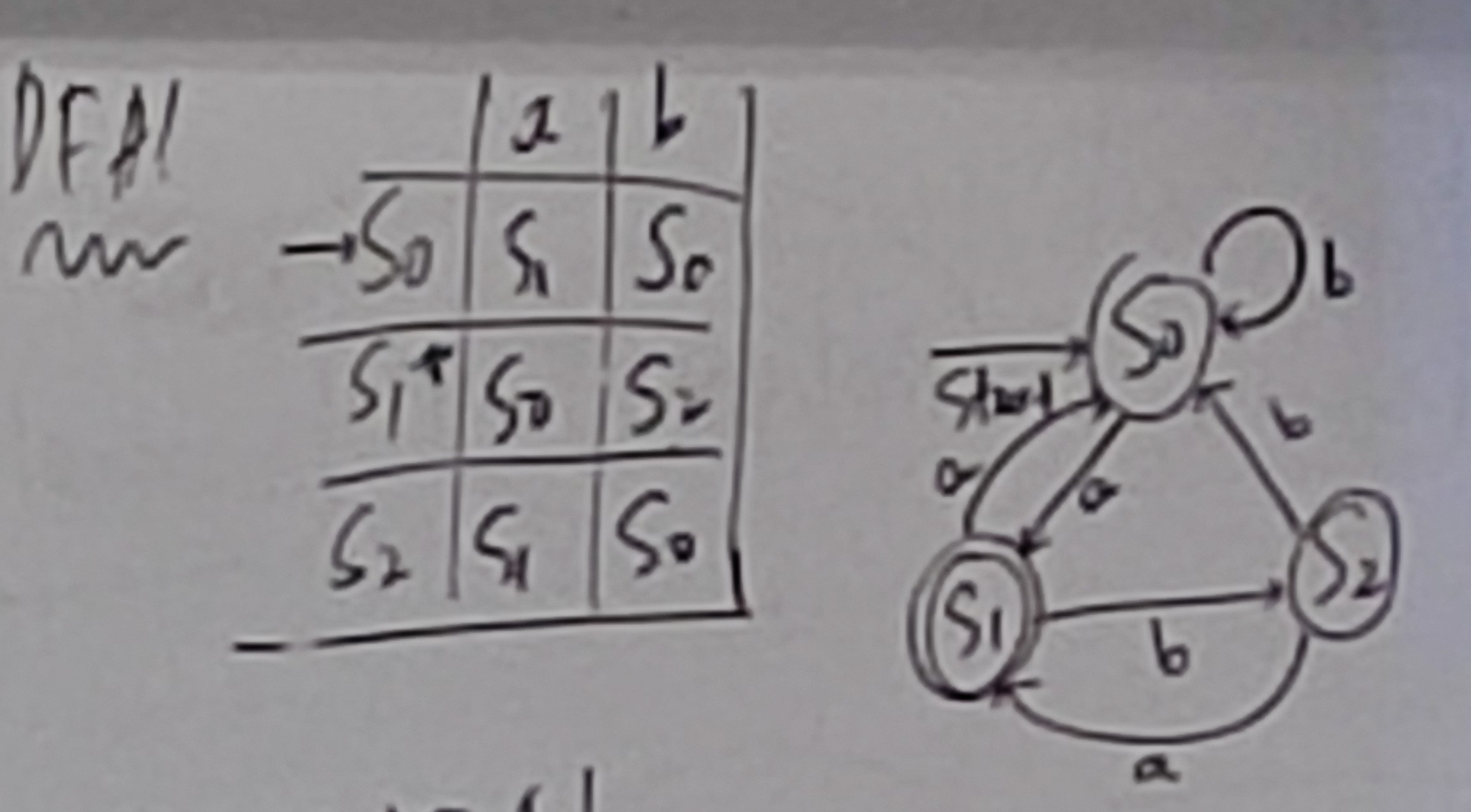
DFA

Given the same input, the resulting state will always be the same.

• A is a start state (has an arrow)
• D is a final state (has an asterisk)
  

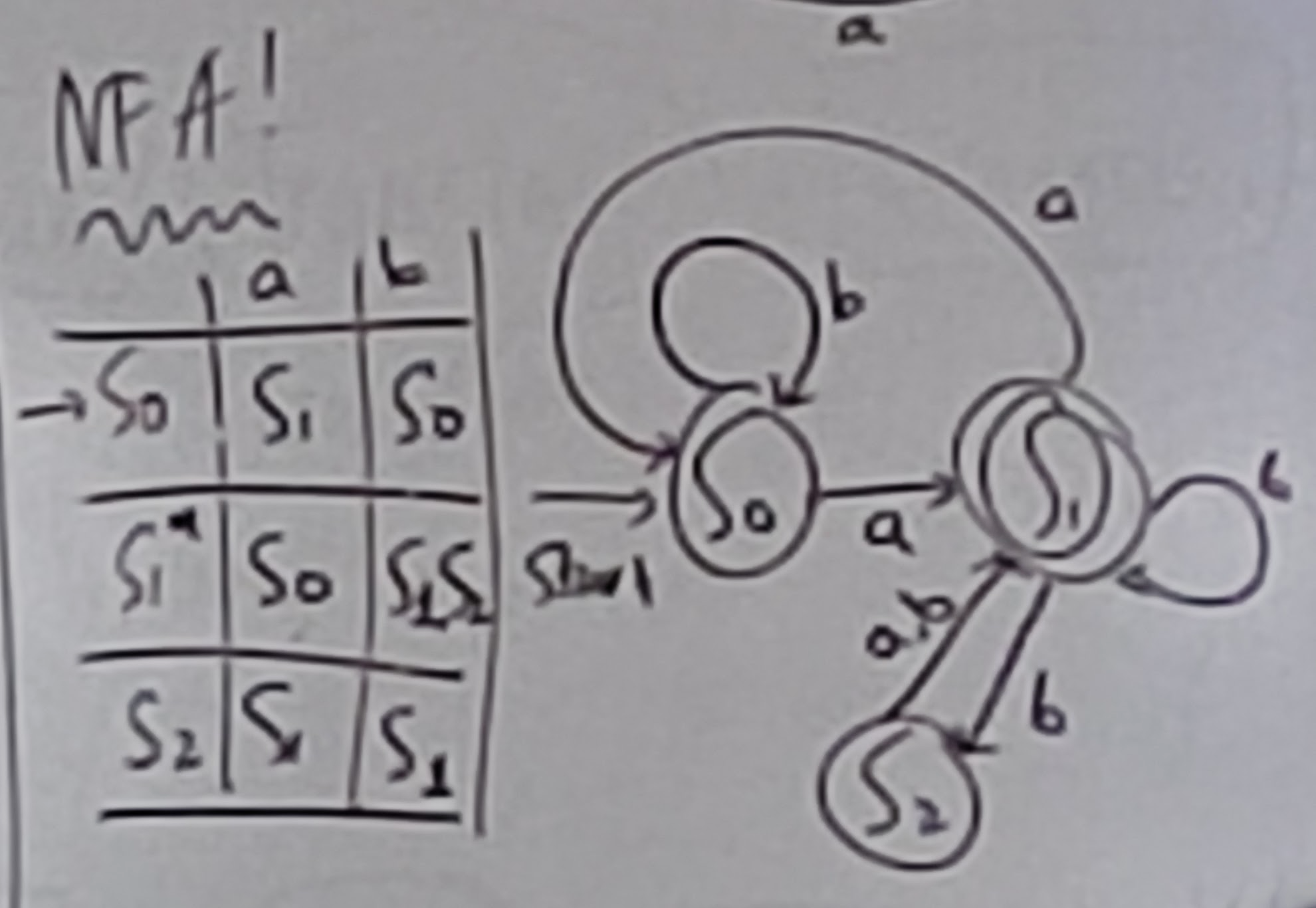
NFA

Conversions

1. RE -> DFA
2. RE -> empty NFA -> DFA
3. NFA -> DFA

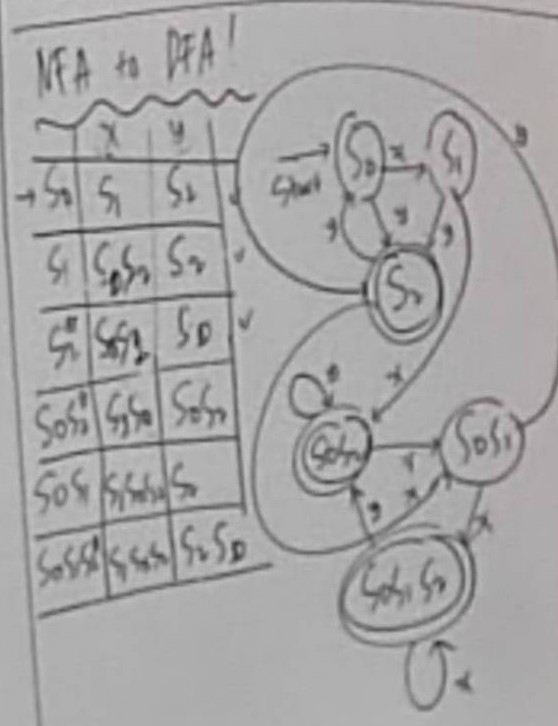
NFA to DFA

1. Membuat state baru untuk state percabangan di table (YANG BELUM ADA VARIABLE/STATE DI TABLE).
2. S1 dikasih X ke S0 dan S1 dikasih X ke S2 maka dijadikan S0S2 jadi state baru.
3. Begitu juga dengan state S0S1.
4. Untuk S0S2 di tabel, kita lihat S0 Diambil X (S1) dan S2 Diambil X (S0S1) maka dapat hasil gabungan keduanya (since S1 muncul 2x cukup ditulis sekali saja) menjadi "S0S1".
5. Ulangi untuk semuanya
6. Selesai ketika Gabungan X/Y sudah ada di Kolom tabel (Variable Table/State).
7. Kalau state baru mengandung final state, maka state tersebut menjadi final state. (i.e. S0S2 jadi final state juga).
   

RE to DFA

1. Tambahkan augmented variable (#) di akhir expression
2. Tambahkan konkatenasi (.) pada expression (. ditambahkan diantara variabel yang tidak memiliki |)
3. Beri nomor pada setiap variabel
4. Tentukan nilai followpos(ition)

(a|b)*a#
 1 2  34

followpos 1 --> aa, ab, aba, aaa
				11  12  123  113 --> ada 1, 2, 3 (followpos 1 adalah 1, 2, 3)

followpos 2 --> bb, ba, ba, baa
			    22  21  23  213 --> ada 1, 2, 3 (followpos 2 adalah 1, 2, 3)

followpos 3 --> # 
			   4 --> followpos 3 adalah 4

followpos 4 --> -
				- --> tidak ada
				

1. Buat tree (kumpulan node)
   • Node -> O (lingkaran)
   • Variabel/Leaf -> tidak punya tangan
   • Simbol -> 2 tangan (. atau |)
   • Closure -> 1 tangan (*, +, atau ?)
2. Beri nomor pada leaf (paling bawah)
3. Tentukan nilai firstpos, lastpos, dan nullable
   • firstpos -> angka pada depan node
     • leaf -> sesuai angka leaf
     • simbol | -> gabungan firstpos node depan (1) dan belakang (2) -> 1,2
     • simbol . -> jika nullable node _depan_ FALSE, firstpos depan, else gabungan
     • closure -> sesuai bawahnya
   • lastpos -> angka pada belakang node
     • leaf -> sesuai angka leaf
     • simbol | -> gabungan lastpos node depan (1) dan belakang (2) -> 1,2
     • simbol . -> jika nullable node _belakang_ FALSE, lastpos belakang, else gabungan
     • closure -> sesuai bawahnya
   • nullable -> node bisa bernilai null atau tidak (TRUE|FALSE)
     • leaf -> pasti FALSE kecuali empty
     • simbol | -> TRUE jika _salah satu_ node bawah TRUE, else FALSE
     • simbol . -> TRUE jika _kedua_ node bawah TRUE, else FALSE
     • closure *, ? -> pasti TRUE, bisa menghasilkan empty
     • closure + -> sesuai bawahnya
4. Buatlah tabel DFA
   • firstpos paling atas adalah S0 (start) pada DFA
   • isi dari variabel (a) adalah gabungan followpos variabel (fp (1,3) -> 1,2,3,4)
   • jika ada angka dari # maka final state
     

RE to e-NFA to DFA

1. Buat empty-NFA
   
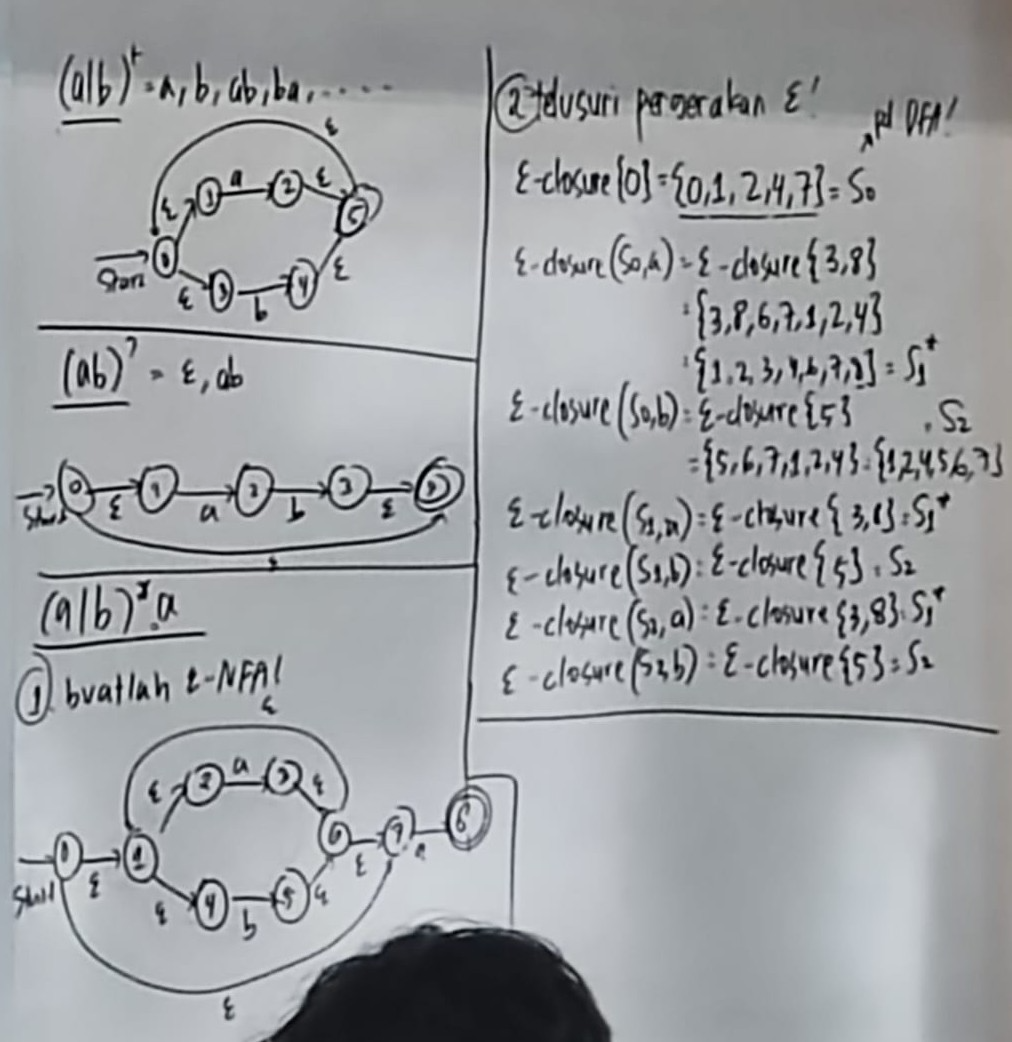
2. Telusuri pergerakan empty

e-closure[0] = { 0, 1, 2, 4, 7 } -> _S0_ (start)
-> semua tujuan yang bisa ditelusuri melalui empty

e-closure(S0, a) = e-closure{3, 8}
-> semua tujuan dari S0 yang bisa diberi 'a'
e-closure(S0, a) = { 1, 2, 3, 4, 6, 7, 8 } -> _S1_
-> setiap angka dari hasil S0 diberi 'a' ditelusuri empty 

e-closure(S0, b) = e-closure{5}
-> semua tujuan dari S0 yang bisa diberi 'b'
e-closure(S0, b) = { 1, 2, 4, 5, 6, 7 } -> _S2_
-> setiap angka dari hasil S0 diberi 'b' ditelusuri empty

e-closure(S1, a) = e-closure{3, 8}
-> semua tujuan dari S1 yang bisa diberi 'a'
e-closure(S1, a) = _S1_
-> e-closure{3, 8} sudah ada di atas sebagai S1

e-closure(S1, b) = e-closure{5}
-> semua tujuan dari S1 yang bisa diberi 'b'
e-closure(S0, b) = _S2_
-> e-closure{5} sudah ada di atas sebagai S2

e-closure(S2, a) = e-closure{3, 8}
-> semua tujuan dari S2 yang bisa diberi 'a'
e-closure(S2, a) = _S1_
-> e-closure{3, 8} sudah ada di atas sebagai S1

e-closure(S2, b) = e-closure{5}
-> semua tujuan dari S2 yang bisa diberi 'b'
e-closure(S0, b) = _S2_
-> e-closure{5} sudah ada di atas sebagai S2

3. Buatlah tabel DFA

4. Gambarkan DFA